Пытка для ума от третьеклассника из Казахстана, в силах ли ты решить
Мой любимый учитель математики Петр Земсков то и дело подкидывает нам пищу для ума. Недавно на своем YouTube-канале он предложил подписчикам решить задачу для третьего класса. Казалось бы, неужели это может быть сложно? В этом-то и вся прелесть!

Школьники щелкают подобные задачки как орешки. Взрослым же приходится поднапрячь извилины, чтобы отыскать правильный ответ. Интересно, а у тебя получится?
Решить задачу третьего класса
Первым делом предлагаю тебе взглянуть на задачу, которую нам сегодня предстоит решить. Подумай, с чего начать и как лучше всего подойти к решению примера так, чтобы сделать это быстрее всего. А затем я расскажу, как ее решил сам учитель математики.

Петр Земсков — опытный учитель математики. Потому, когда ему позвонил его племянник из Казахстана и предложил решить задачу третьего класса, мужчина тут же откликнулся. Только загвоздка в том, что решать он начал по-взрослому.
Земсков определил, что в примере есть три переменных. Тут же делаем паузу. Почему три, а не четыре? Всё просто! Два примера из четырех в результате дают 8. К числу, которое находится в правом верхнем квадрате нужно прибавить одно и то же число, чтобы получить 8.

Это знание помогло Петру составить систему и представить неизвестные переменные в таком виде: x + y = 8, x + z = 13, z – x = 6. И вот на этом этапе математик осознал, что третьеклассники подобные уравнения решать еще не умеют. Значит, должен быть более простой и доступный способ.
Телефонный звонок. На том конце провода раздается звонкий детский голос: «Мы дроби не учили еще. Но мы учили половинки!» Вот тебе и ответ на все вопросы. Земсков возвращается к решению задачи третьего класса и мыслит так, как должен мыслить школьник.
Решение задачи с тремя неизвестными
Учитель подходит к решению задачи через игру: «Если весы в равновесии, то чаши весов мы можем складывать. То же самое с равенствами. Мы можем складывать их левую и правую часть». Петр предлагает сложить пример с ответом 13 и пример с ответом 6. При этом не забываем, что 2 числа из этих примеров одинаковы.

Поскольку в первом примере (с ответом 13) мы видим сложение, а во втором — вычитание, одинаковые числа просто исчезнут при сложении. А единственное неизвестное число складывается дважды. «Два вот таких кубика равны тринадцать плюс шесть», — объясняет учитель, показывая на квадрат в левом нижнем углу. 13 + 6 = 19, а 19 ÷ 2 = 9,5.
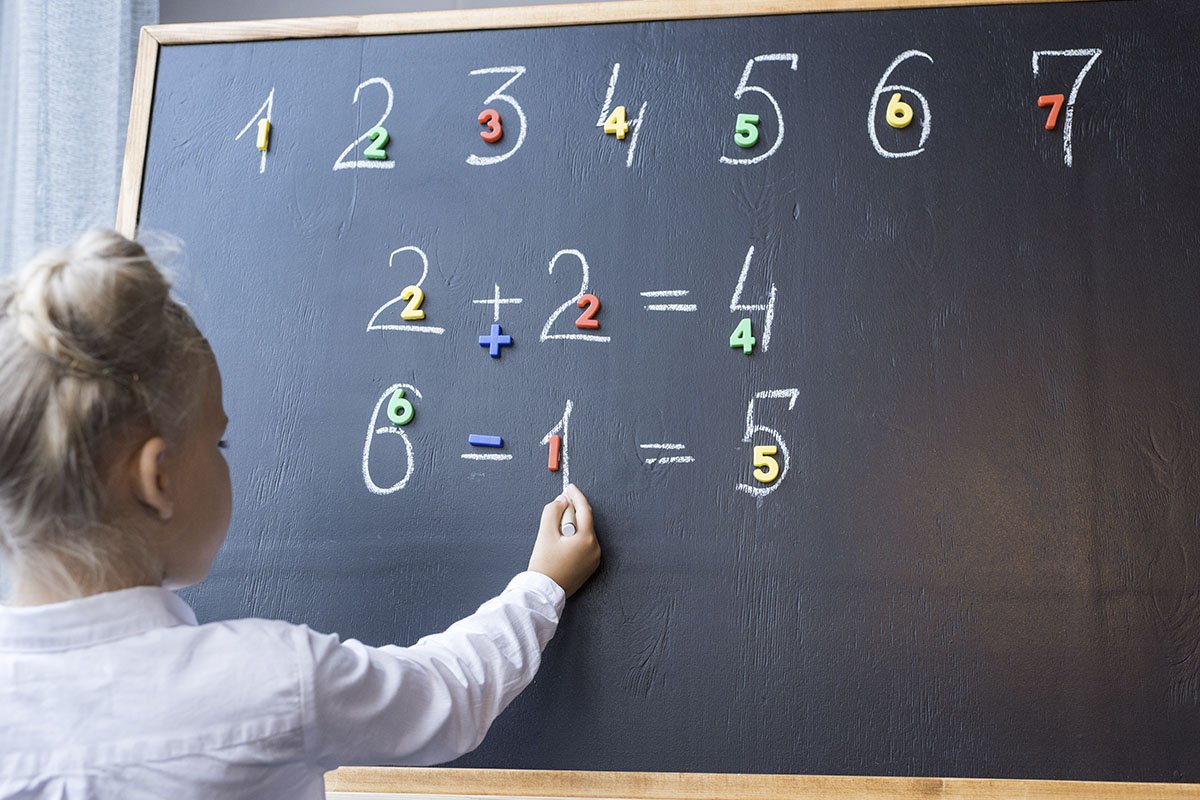
Ну а дальше всё решается очень просто. Подставляем 9,5 в нужное место и считаем, сколько нужно отнять от этого числа, чтобы получилось 6. Действие простое, потому нам даже записывать его не нужно.
В результате получаем: 9,5 – 3,5 = 6. Вспоминаем, что числа в нижнем правом и верхнем левом квадрате одинаковые. Нам остается выяснить, что находится в последнем квадрате. Получаем: 3,5 + 4,5 = 8.
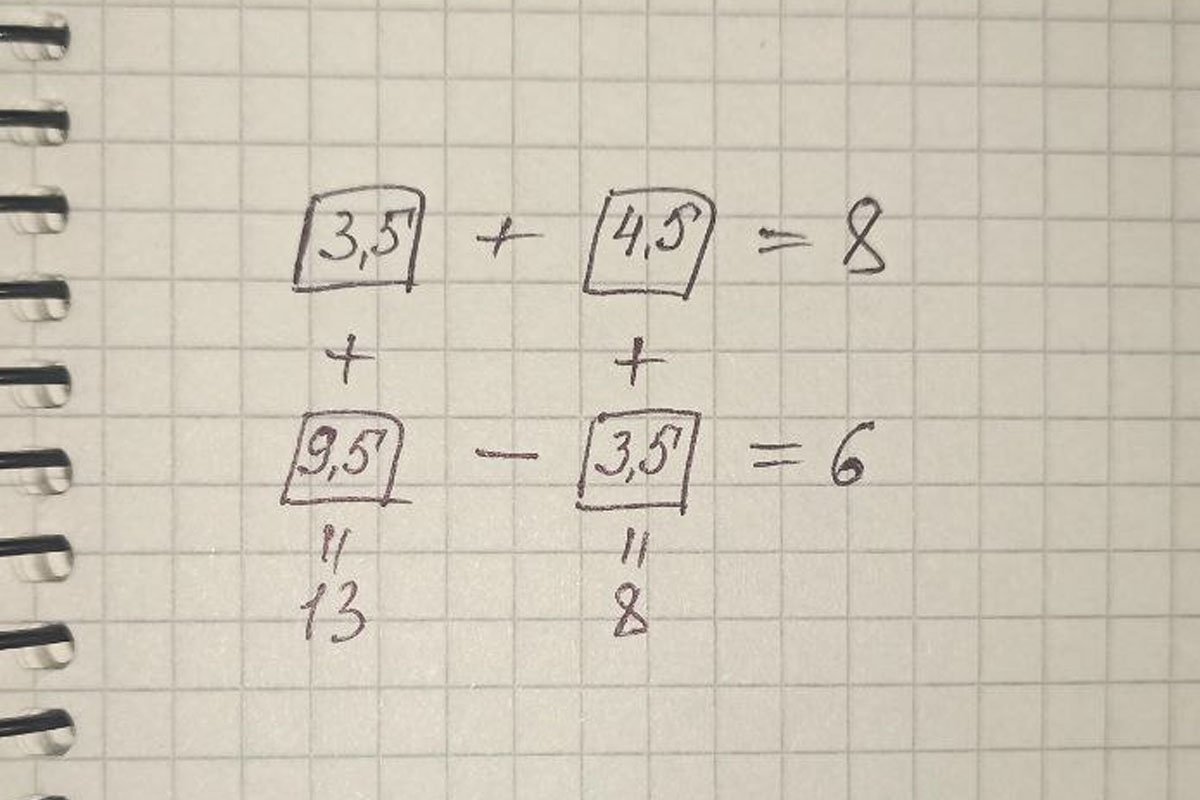
Расскажи, а тебе удалось решить эту задачку? Кстати, будет здорово, если ты покажешь пример своим детям. Поделись в комментариях, получилось ли у них с ним справиться. Ждем тебя внизу!

Школьники щелкают подобные задачки как орешки. Взрослым же приходится поднапрячь извилины, чтобы отыскать правильный ответ. Интересно, а у тебя получится?
Решить задачу третьего класса
Первым делом предлагаю тебе взглянуть на задачу, которую нам сегодня предстоит решить. Подумай, с чего начать и как лучше всего подойти к решению примера так, чтобы сделать это быстрее всего. А затем я расскажу, как ее решил сам учитель математики.

Петр Земсков — опытный учитель математики. Потому, когда ему позвонил его племянник из Казахстана и предложил решить задачу третьего класса, мужчина тут же откликнулся. Только загвоздка в том, что решать он начал по-взрослому.
Земсков определил, что в примере есть три переменных. Тут же делаем паузу. Почему три, а не четыре? Всё просто! Два примера из четырех в результате дают 8. К числу, которое находится в правом верхнем квадрате нужно прибавить одно и то же число, чтобы получить 8.

Это знание помогло Петру составить систему и представить неизвестные переменные в таком виде: x + y = 8, x + z = 13, z – x = 6. И вот на этом этапе математик осознал, что третьеклассники подобные уравнения решать еще не умеют. Значит, должен быть более простой и доступный способ.
Телефонный звонок. На том конце провода раздается звонкий детский голос: «Мы дроби не учили еще. Но мы учили половинки!» Вот тебе и ответ на все вопросы. Земсков возвращается к решению задачи третьего класса и мыслит так, как должен мыслить школьник.
Решение задачи с тремя неизвестными
Учитель подходит к решению задачи через игру: «Если весы в равновесии, то чаши весов мы можем складывать. То же самое с равенствами. Мы можем складывать их левую и правую часть». Петр предлагает сложить пример с ответом 13 и пример с ответом 6. При этом не забываем, что 2 числа из этих примеров одинаковы.

Поскольку в первом примере (с ответом 13) мы видим сложение, а во втором — вычитание, одинаковые числа просто исчезнут при сложении. А единственное неизвестное число складывается дважды. «Два вот таких кубика равны тринадцать плюс шесть», — объясняет учитель, показывая на квадрат в левом нижнем углу. 13 + 6 = 19, а 19 ÷ 2 = 9,5.
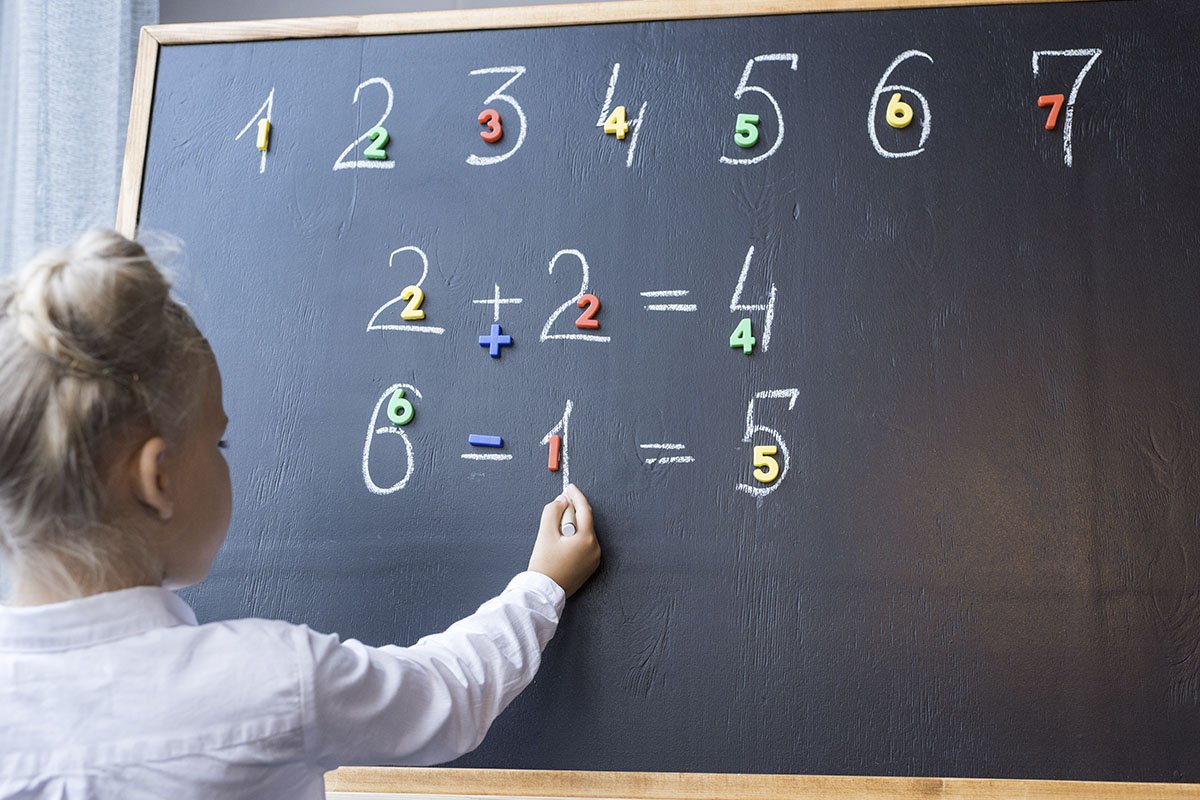
Ну а дальше всё решается очень просто. Подставляем 9,5 в нужное место и считаем, сколько нужно отнять от этого числа, чтобы получилось 6. Действие простое, потому нам даже записывать его не нужно.
В результате получаем: 9,5 – 3,5 = 6. Вспоминаем, что числа в нижнем правом и верхнем левом квадрате одинаковые. Нам остается выяснить, что находится в последнем квадрате. Получаем: 3,5 + 4,5 = 8.
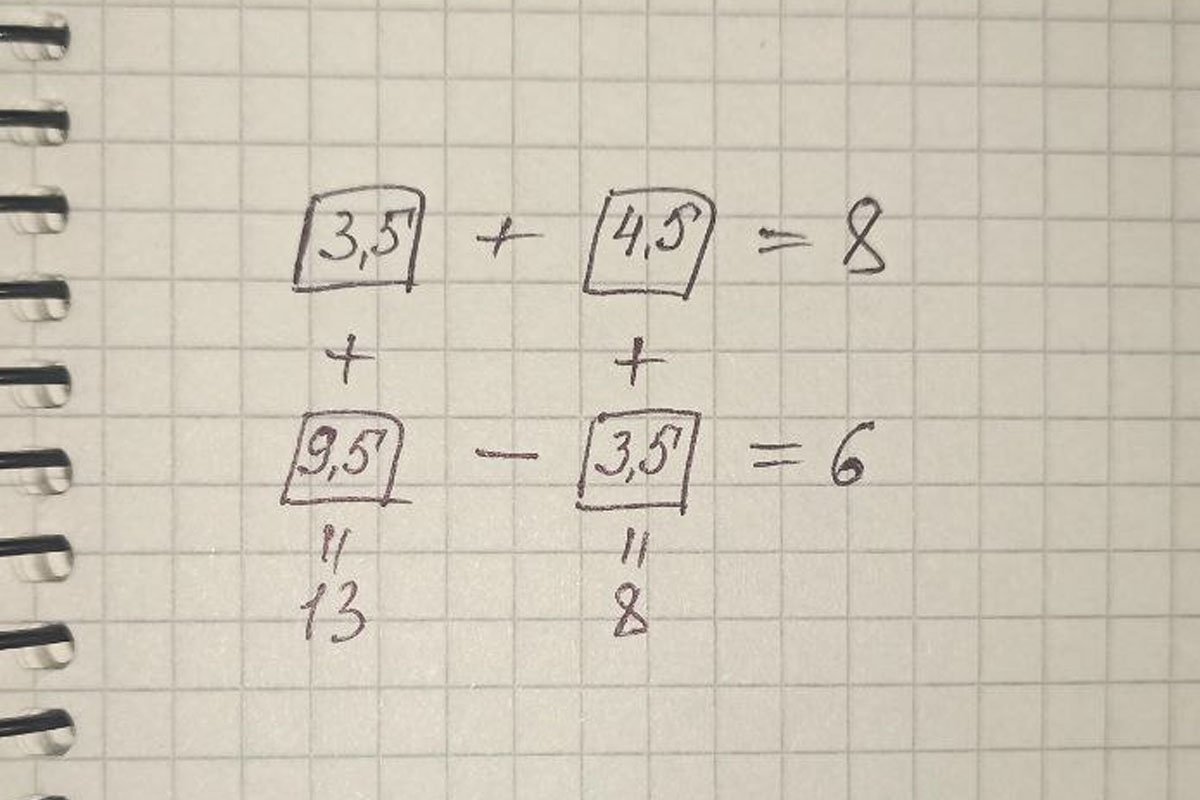
Расскажи, а тебе удалось решить эту задачку? Кстати, будет здорово, если ты покажешь пример своим детям. Поделись в комментариях, получилось ли у них с ним справиться. Ждем тебя внизу!